Date: 2018-06-14
Categories: research; parsing

A typed DSL for parsing

I have played around with various forms of parsing for many years. ("Too many" most other researchers would say at this point.) Recently I have been looking at alternatives to combinator parsing. The aim is to have a DSL which captures all the nice things about combinator parsing (type inference, type checking, flexibility etc) but without committing to the parsing strategy employed by combinator parsing (parse prefixes of the string - this is inefficient for obvious reasons).

My current best effort can be found in the p1_extra GitHub repository. For a grammar like this:

S -> E eof
E -> E E E 
E -> "1"
E -> eps

With actions which compute the "sum" of the span parsed:

S -> E  eof {{ fun (x,_) -> x }}
E -> E E E  {{ fun (x,y,z) -> x+y+z }}
E -> "1"  {{ fun _ -> 1 }}
E -> eps  {{ fun _ -> 0 }}

The OCaml code looks like this:



(* S -> E; E -> E E E | "1" | eps *)

_S -->rhs2 
  (nt _E, eof)  (fun (x,_) -> x);

_E -->rhs3
  (nt _E,nt _E, nt _E)  (fun (x,y,z) -> x+y+z);

_E -->rhs1 
  (a "1")  (fun _ -> 1);

_E -->rhs1 
  eps  (fun _ -> 0);

Compared to the informal version, we can see that there is an injection nt from nonterminals to "elements" (things that can appear as part of the rhs of a production). Also, we have to give the arity of the production explicitly (rhs1, rhs2 etc). Otherwise this looks pretty good.

The point is: from this definition we can generate a combinator parser, but we can also generate eg an Earley parser, or any other kind of parser. Moreover, the IDE (merlin/tuareg) will identify any type mistakes (or arity mistakes) we make while defining the grammar. So this seems pretty close to optimal for a grammar-with-actions parsing DSL.

Another example, perhaps more compelling, is lambda calculus:

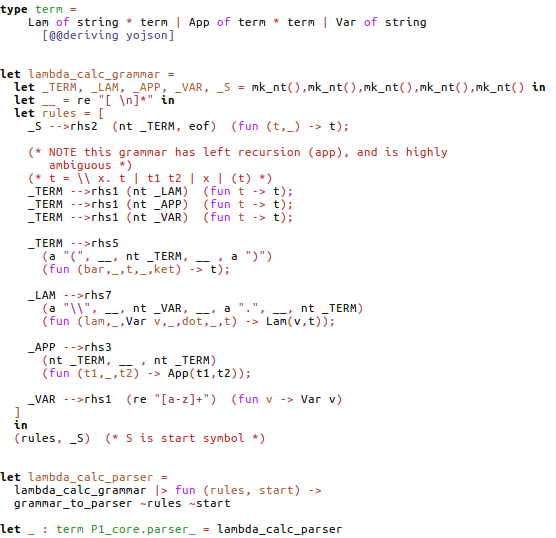
Note that the grammar spec has left recursion and is highly ambiguous. Even so, this spec can be transformed into a parser in a very straightforward way - by applying grammar_to_parser to the rules and the start symbol (this is the defn. of lambda_calc_parser).